Menu
PHP/Javascript/HTML and Python PyEphem Moon Angle Tutorial
A long time ago now we presented PHP/Javascript/HTML Moon Angle Tutorial but now we feel is a good time for it to get a makeover. Why is that? Well, we have the relatively new discovery of the very useful Python PyEphem module to thank for that.
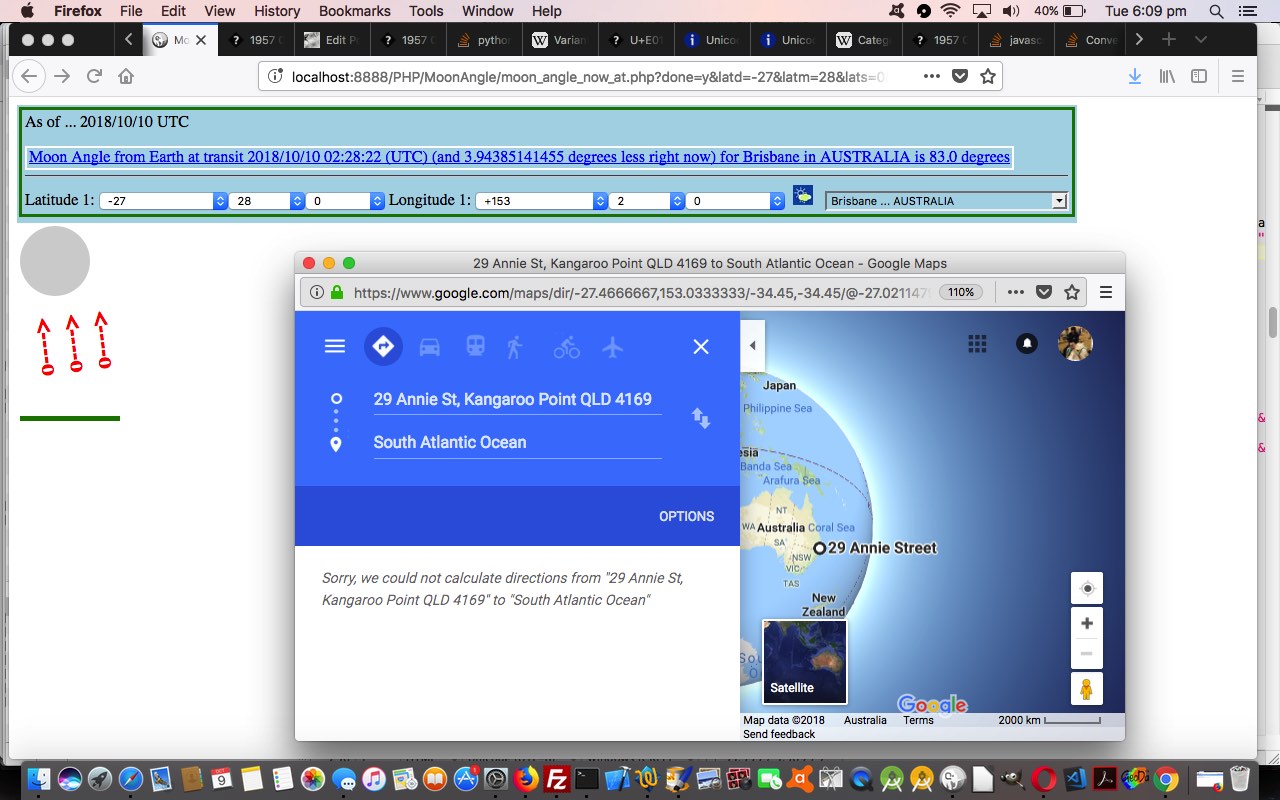
As far as the new version goes we now offer a Moon Angle โtime of transit (and relative to now)โ calculation, which we think will be of more use to users.
The Moon Angle at Transit calculations again involve the Sublunary Point as the position on Earth directly above which is Moon is located. Add in the Python PyEphem work and some more terminology that may interest you could involve โฆ
โฆ within the Python of interest, a snapshot of which is shown below, but which changes each time somebody recreates this sublunarx.py โฆ
import ephem
import math
import time
from datetime import datetime, timedelta
greenwich = ephem.Observer()
greenwich.lat = "0"
greenwich.lon = "0"
greenwich.date = datetime.utcnow()
moon = ephem.Moon(greenwich)
moon.compute(greenwich.date)
moon_lon = math.degrees(moon.ra - greenwich.sidereal_time() )
if moon_lon < -180.0 :
moon_lon = 360.0 + moon_lon
elif moon_lon > 180.0 :
moon_lon = moon_lon - 360.0
moon_lat = math.degrees(moon.dec)
d1 = ephem.next_full_moon(greenwich.date)
d2 = ephem.next_new_moon(greenwich.date)
greenwich.lat = "151:10.586502000000001"
greenwich.lon = "-33:54.445878"
greenwich.date = datetime.utcnow()
moon = ephem.Moon(greenwich)
moon.compute(greenwich.date)
betw = (greenwich.next_transit(moon) - greenwich.date) * 86400.0 / 60.0 / 60.0
gnt = greenwich.next_transit(moon)
greenwich.date = gnt
moon = ephem.Moon(greenwich)
moon.compute(gnt)
moon_lon_x = math.degrees(moon.ra - greenwich.sidereal_time() )
if moon_lon_x < -180.0 :
moon_lon_x = 360.0 + moon_lon_x
elif moon_lon_x > 180.0 :
moon_lon_x = moon_lon_x - 360.0
moon_lat_y = math.degrees(moon.dec)
print('%s %s %s %s %s %s %s %f' % (moon_lon, moon_lat, d1, d2, gnt, moon_lon_x, moon_lat_y, betw))
quit()
The Moon Angle web application live
run, which we welcome you to try, has the underlying PHP moon_angle_now_at
php that supervises the Python exemplied above, and which featured thesechanges to make this happen.
Previous relevant PHP/Javascript/HTML Moon Angle Tutorial is shown below.
PHP/Javascript/HTML Moon Angle Tutorial
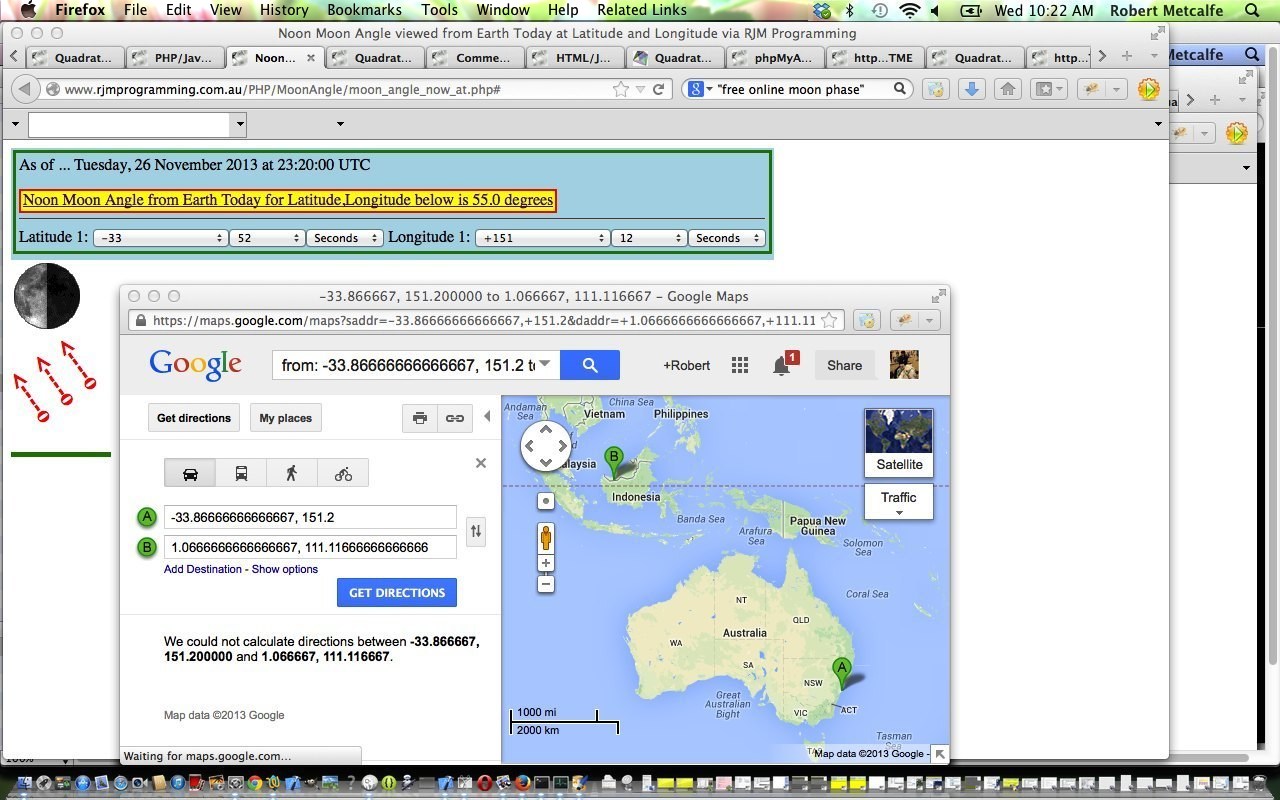
Here is a tutorial that calculates Noon Moon Angles from Earth via the entry of Latitude and Longitude. The calculation of noon moon angles uses the concept of Sublunary Point, which is explained in the quote from Wikipedia below.
The sublunary point (Latin sub-lunar, under the moon โ, from Latin) is the one place on earth where the moon in exactly the zenith is. He is the point where the line connecting the centers of the Earth and Moon intersects the Earthโs surface. The point is a common auxiliary point to observe the Moon in the celestial mechanics and astronomical phenomenology , and in particular the theory of the tides , as well as the theory of eclipses .
The calculation of the point corresponding to the determination of the geocentric coordinates of the Moon, it has the same longitude and latitude , as the moon astronomical length and width has โ both are denoted by ฯ and ฮฒ.
The Javascript embellishments in this tutorial mainly revolve around:
The use of window.open can sometimes be blocked by web browsers depending on their settings and you can read a bit more about such issues here.
Useful tutorials that helped, and we give thanks to, were:
- Sublunary Point (information from Wikipedia, from where quote above comes)
- Sublunary Point calculator helper via cURL
- Moon Phase calculator helper via cURL
- Sun Angle formulae applied to the case of the Moon Sublunary Point
- Sydney positioning
- CSS 2D Transformation Rotations
Here is a link to a liverun. (The way it changed on 1/12/2013 to have a dropdown of placenames as extra functionality will be explained in a tutorial called PHP/Javascript/HTML Geographical Placename Integration Tutorial on 3/12/2013.)
Here is a link to some downloadable PHP programming source code which you may want to rename to moon_angle_now_atphp
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.
