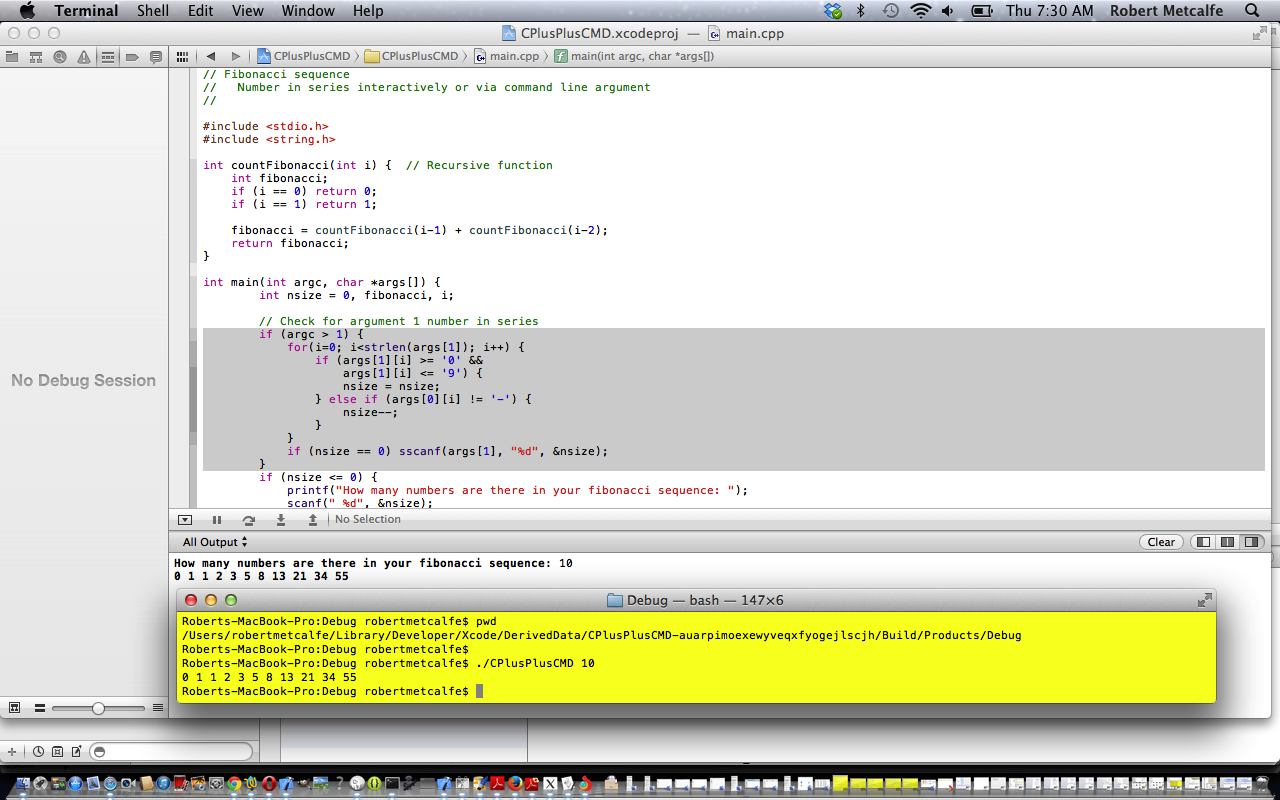
Back in October, 2013 we presented C Recursion Primer Tutorial as a C++ ( but really just straight C code) Xcode (IDE) project on Mac OS X. That’s a long time ago, looking at it from late in 2021. So what’s the go now with …
- macOS Big Sur v11.6 …
- Xcode Version 13.0 (13A233)
… and while we are there, tweak the main.cpp code because we’ve never found a “project revisit” yet, where we didn’t want to change something.
You might be pleased to know that the Xcode Version 13.0 (13A233) way to setup this project …
- click Xcode (macOS desktop) icon
- File -> New -> Project…
- macOS (tab) … Application (section) … Command Line Tool … click Next
- Product Name … fill in a suitable project name (eg. Fibonacci)
- Language -> C … click Next
- we just edited the project’s main.c for today’s “Fibonacci series revisit with delimitation selection“
… does not require any “code signing”. Forgotten what C looks like? A really simple C “main.c” can look like …
// Fibonacci sequence
// Number in series interactively or via command line argument
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int countFibonacci(int i) { // Recursive function
int fibonacci;
if (i == 0) { return 0; } else if (i == 1) { return 1; }
fibonacci = countFibonacci(i-1) + countFibonacci(i-2);
return fibonacci;
}
int main(int argc, char *args[]) {
char delim[3]=", \0";
int nsize = 0, fibonacci, i;
// Check for argument 1 number in series
if (argc > 1) {
for(i=0; i<strlen(args[1]); i++) {
if (args[1][i] == '-' || (args[1][i] >= '0' && args[1][i] <= '9')) {
nsize = nsize;
} else if (args[0][i] != '-') {
nsize--;
}
}
if (nsize == 0) sscanf(args[1], "%d", &nsize);
}
if (argc <= 1) { //nsize <= 0) {
printf("How many numbers are there in your fibonacci sequence (-ve for in a row): ");
scanf(" %d", &nsize);
}
if (nsize > 0) { strcpy(delim, "\n\0"); }
for (i=0; i<=(int) abs(nsize); i++) {
fibonacci = countFibonacci(i);
if (i == (int) abs(nsize)) { printf("%d", fibonacci); } else { printf("%d%s", fibonacci, delim); }
}
printf("\n");
}
Did you know?
Am sure we can hear a lot of you say …
Isn’t the “Command Line” bit of “Command Line Tool” a bit removed from how you Run the C program in Xcode?
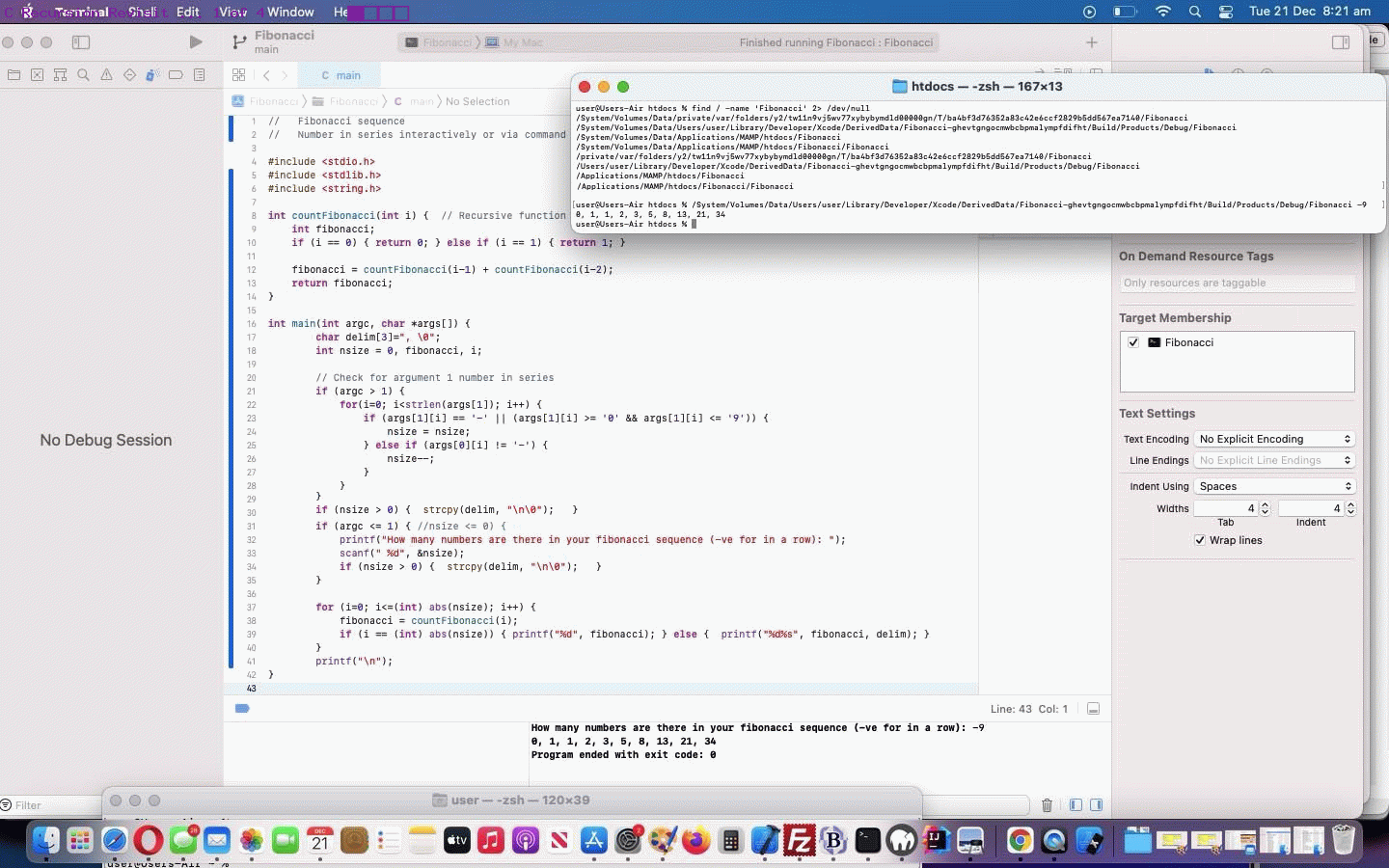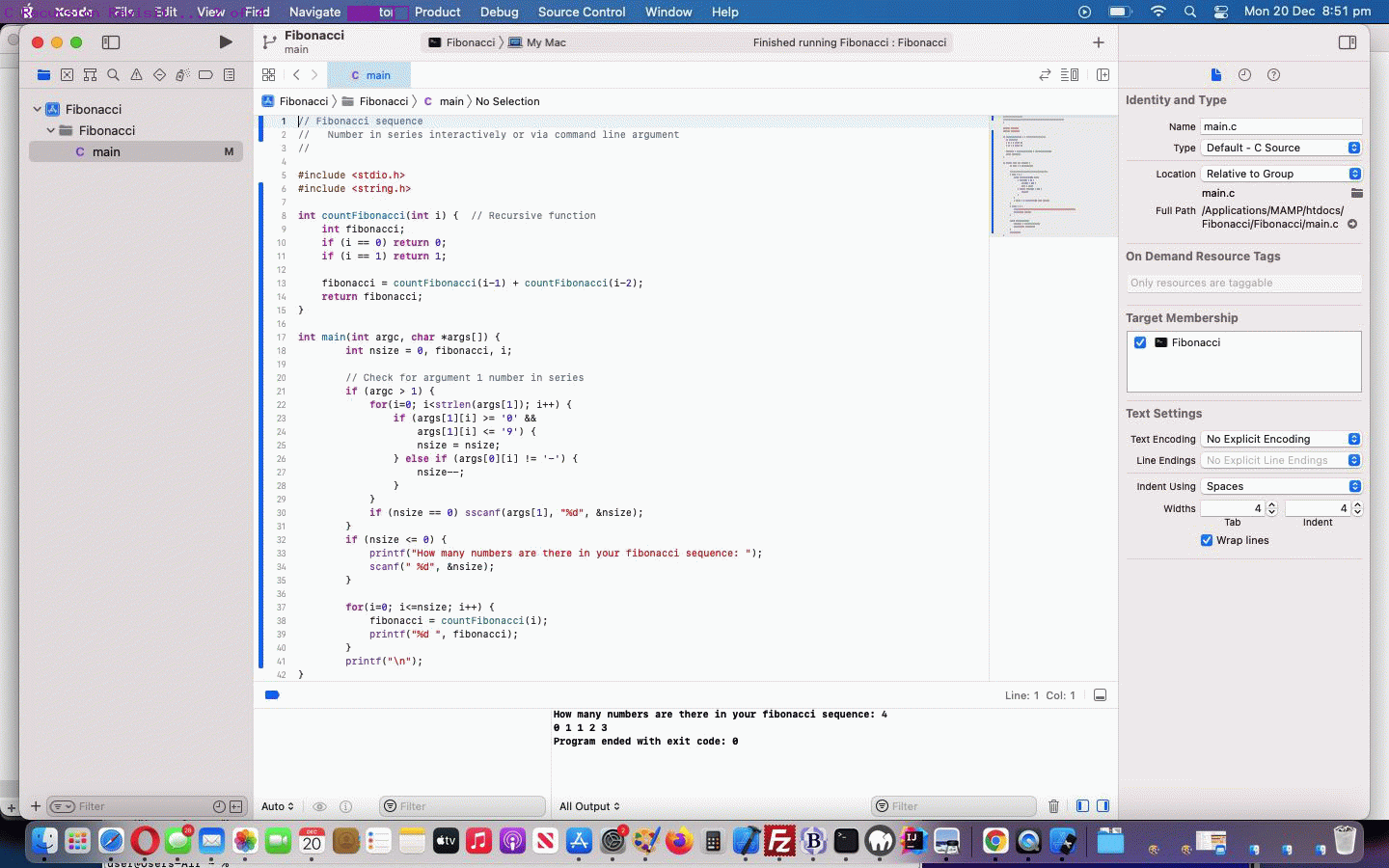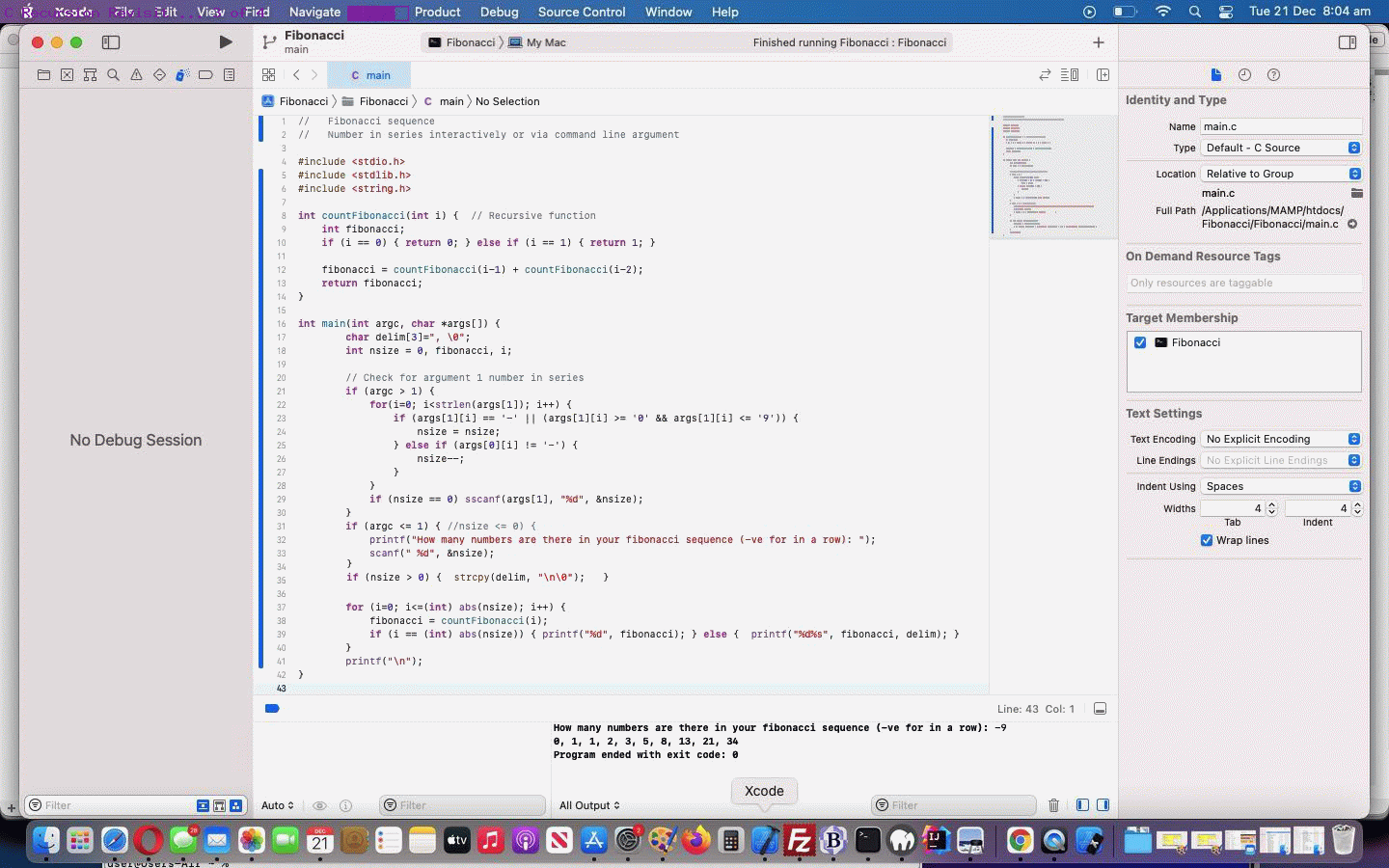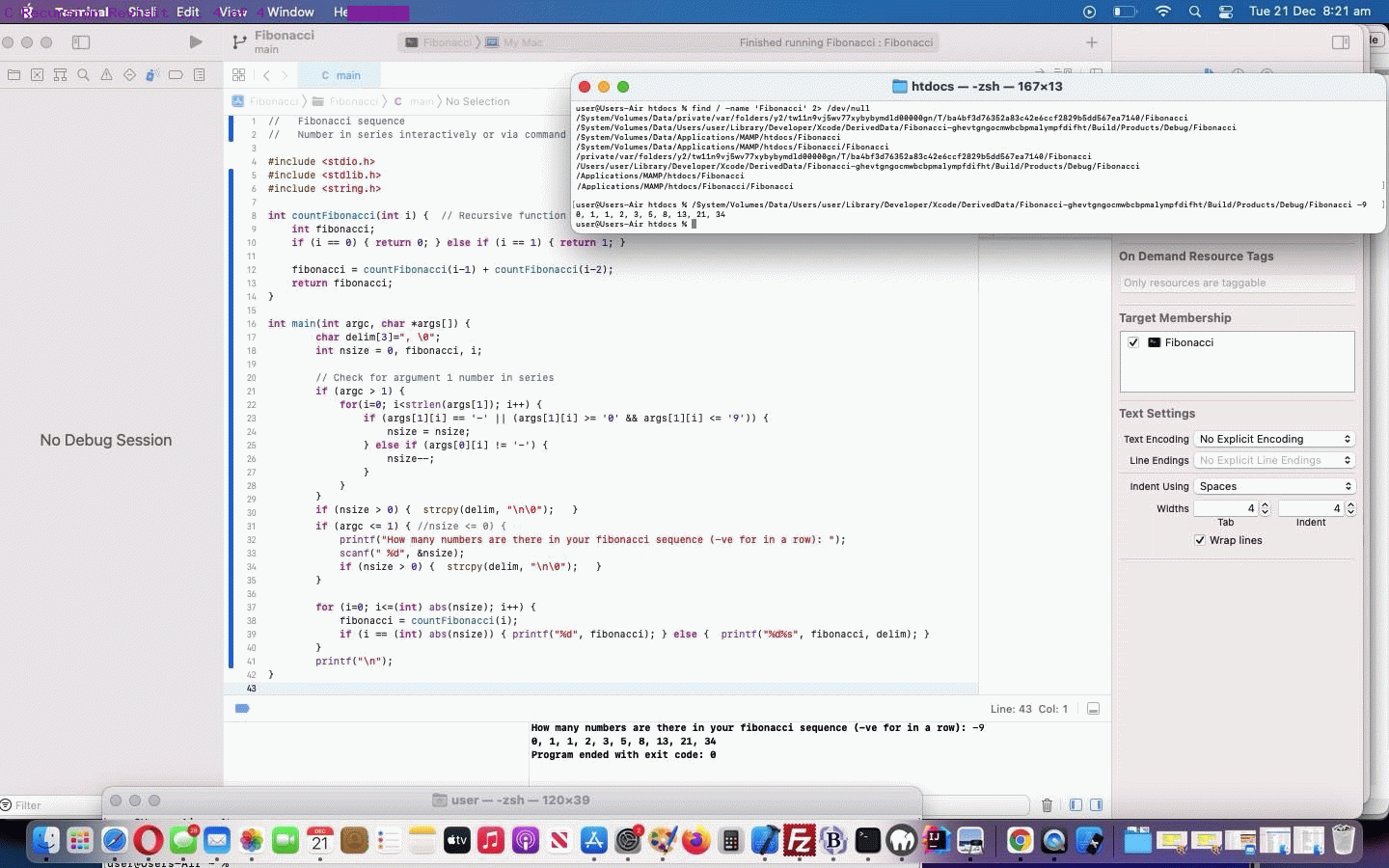
We’d agree. But every time you successfully Compile in Xcode a C (or C++) program, behind the scenes a [ProjectName] executable is created in a folder on your macOS computer. We found where via …
find / -name 'Fibonacci' 2> /dev/null
… “Fibonacci” being our [ProjectName] today … and got back …
/System/Volumes/Data/private/var/folders/y2/tw11n9vj5wv77xybybymdld00000gn/T/ba4bf3d76352a83c42e6ccf2829b5dd567ea7140/Fibonacci
/System/Volumes/Data/Users/user/Library/Developer/Xcode/DerivedData/Fibonacci-ghevtgngocmwbcbpmalympfdifht/Build/Products/Debug/Fibonacci
/System/Volumes/Data/Applications/MAMP/htdocs/Fibonacci
/System/Volumes/Data/Applications/MAMP/htdocs/Fibonacci/Fibonacci
/private/var/folders/y2/tw11n9vj5wv77xybybymdld00000gn/T/ba4bf3d76352a83c42e6ccf2829b5dd567ea7140/Fibonacci
/Users/user/Library/Developer/Xcode/DerivedData/Fibonacci-ghevtgngocmwbcbpmalympfdifht/Build/Products/Debug/Fibonacci
/Applications/MAMP/htdocs/Fibonacci
/Applications/MAMP/htdocs/Fibonacci/Fibonacci
… and ruling out the Xcode project last two places (which are distinct from where Xcode creates the executable) we deduced …
/System/Volumes/Data/Users/user/Library/Developer/Xcode/DerivedData/Fibonacci-ghevtgngocmwbcbpmalympfdifht/Build/Products/Debug/Fibonacci -9
… would get us …
0, 1, 1, 2, 3, 5, 8, 13, 21, 34
… as it should … on the “Command Line” (in Terminal application of macOS).
More macOS command line “find” command refinement thoughts tomorrow!
Previous relevant C Recursion Primer Tutorial is shown below.
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, in which it refers to a method of defining functions in which the function being defined is applied within its own definition. Specifically this defines an infinite number of instances (function values), using a finite expression that for some instances may refer to other instances, but in such a way that no loop or infinite chain of references can occur. The term is also used more generally to describe a process of repeating objects in a self-similar way.
Recursion is not just applicable to C. Already we have shown the same scenario, which you can compare and contrast, here, in Java, with Java Recursion Primer Tutorial, shown below. It is a good technique to use in many programming applications unless its use becomes too esoteric. It is usually true that a non-recursive technique can be used in place of the recursive technique. As you might guess, you can reduce the size of your code using recursion in your code. Recursive functions need an “anal” hard coded return, ahead of time, for the end-of-the-line value returned … as you see here for when i=1 or i=0 … if you don’t do this, it may be that your recursive function contributes to infinite looping … the stuff of nightmares.
Today’s tutorial in C(++) in Xcode shows you a way to find the path to your executable, the knowledge of which can then be applied to run the executable from a (Mac Terminal) Linux bash command line, as shown in the picture above and the last slide of the tutorial.
Link to Recursion information … via Wikipedia (as per information above).
This tutorial shows the use of a recursive function used to show the Fibonacci Sequence of a designated sequence size, both interactively or via (Mac Terminal application Linux bash) command line arguments.
Liber Abaci also posed, and solved, a problem involving the growth of a population of rabbits based on idealized assumptions. The solution, generation by generation, was a sequence of numbers later known as Fibonacci numbers. The number sequence was known to Indian mathematicians as early as the 6th century,[10][11][12] but it was Fibonacci’s Liber Abaci that introduced it to the West.
In the Fibonacci sequence of numbers, each number is the sum of the previous two numbers, starting with 0 and 1. This sequence begins 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 … [13]
The higher up in the sequence, the more closely the ratio of two consecutive Fibonacci numbers will approach the golden ratio (approximately 1 : 1.618 or 0.618 : 1).
Link to Fibonacci Sequence information … via Wikipedia (as per information above).
Link to … Elementary my dear Watson! … wow.
Download programming code and rename to main.cpp or main.c … depending on your environment.
If this was interesting you may be interested in this too.
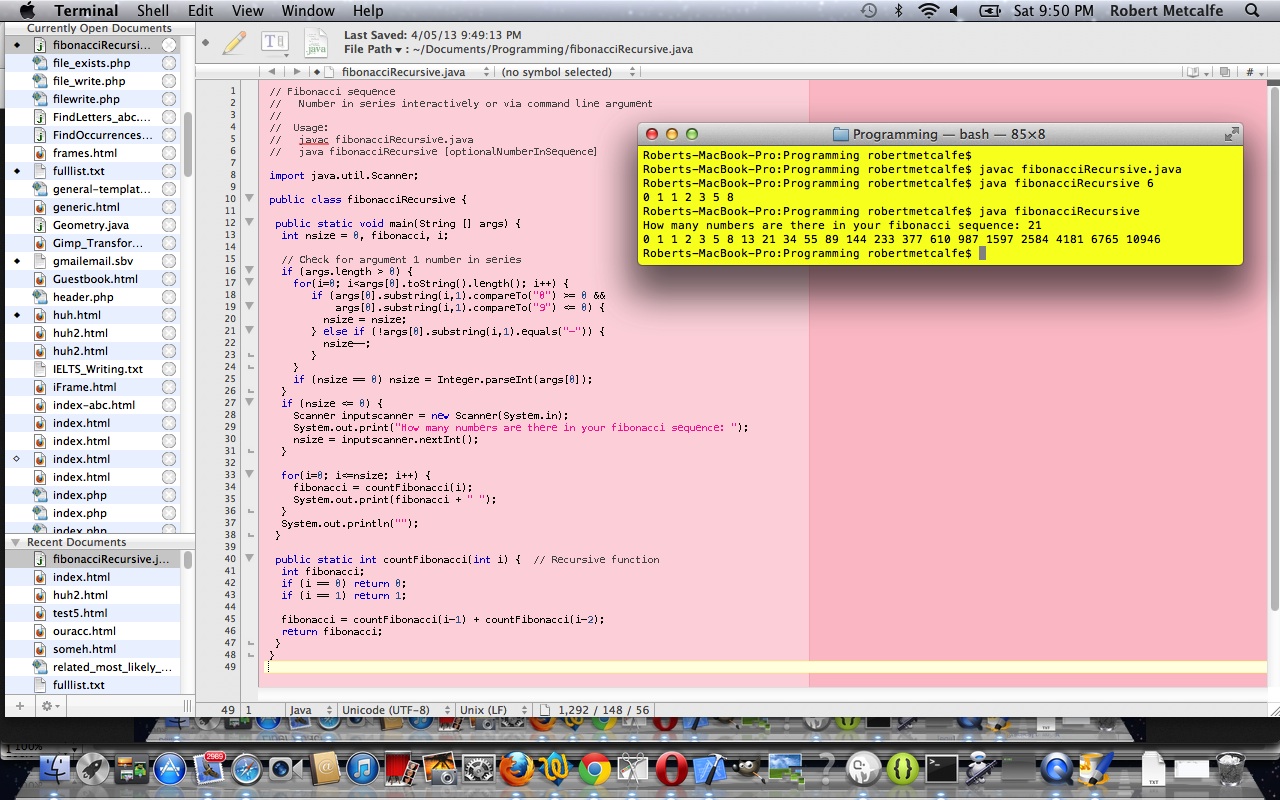
Previous relevant (compare and contrast) Java Recursion Primer Tutorial is shown below.
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, in which it refers to a method of defining functions in which the function being defined is applied within its own definition. Specifically this defines an infinite number of instances (function values), using a finite expression that for some instances may refer to other instances, but in such a way that no loop or infinite chain of references can occur. The term is also used more generally to describe a process of repeating objects in a self-similar way.
Recursion is not just applicable to Java. It is a good technique to use in many programming applications unless its use becomes too esoteric. It is usually true that a non-recursive technique can be used in place of the recursive technique. As you might guess, you can reduce the size of your code using recursion in your code. Recursive functions need an “anal” hard coded return, ahead of time, for the end-of-the-line value returned … as you see here for when i=1 or i=0 … if you don’t do this, it may be that your recursive function contributes to infinite looping … the stuff of nightmares.
Link to Recursion information … via Wikipedia (as per information above).
This tutorial shows the use of a recursive function used to show the Fibonacci Sequence of a designated sequence size.
Liber Abaci also posed, and solved, a problem involving the growth of a population of rabbits based on idealized assumptions. The solution, generation by generation, was a sequence of numbers later known as Fibonacci numbers. The number sequence was known to Indian mathematicians as early as the 6th century,[10][11][12] but it was Fibonacci’s Liber Abaci that introduced it to the West.
In the Fibonacci sequence of numbers, each number is the sum of the previous two numbers, starting with 0 and 1. This sequence begins 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 … [13]
The higher up in the sequence, the more closely the ratio of two consecutive Fibonacci numbers will approach the golden ratio (approximately 1 : 1.618 or 0.618 : 1).
Link to Fibonacci Sequence information … via Wikipedia (as per information above).
Link to … Elementary my dear Watson! … wow.
Download programming code and rename to fibonacciRecursive.java
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.