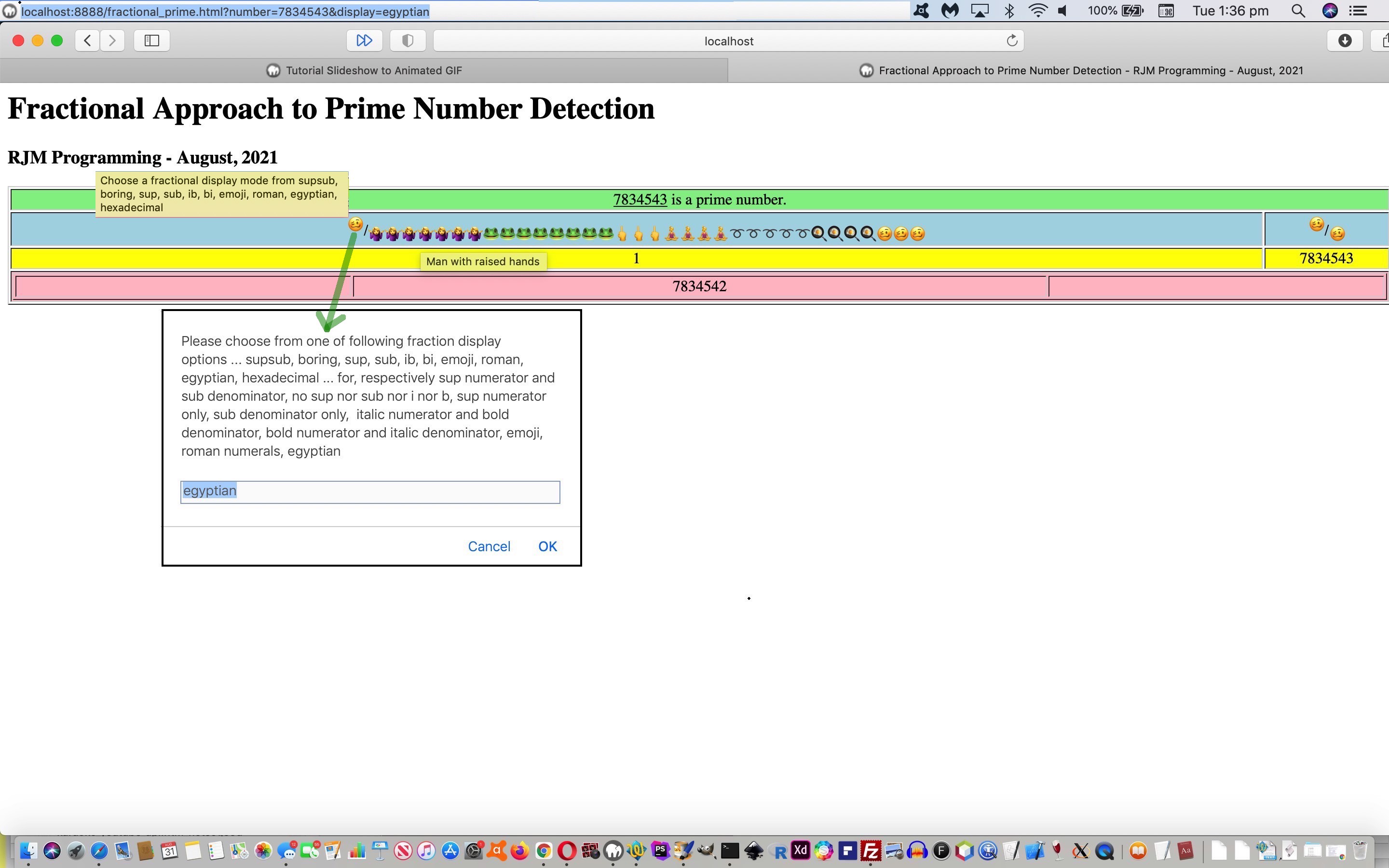
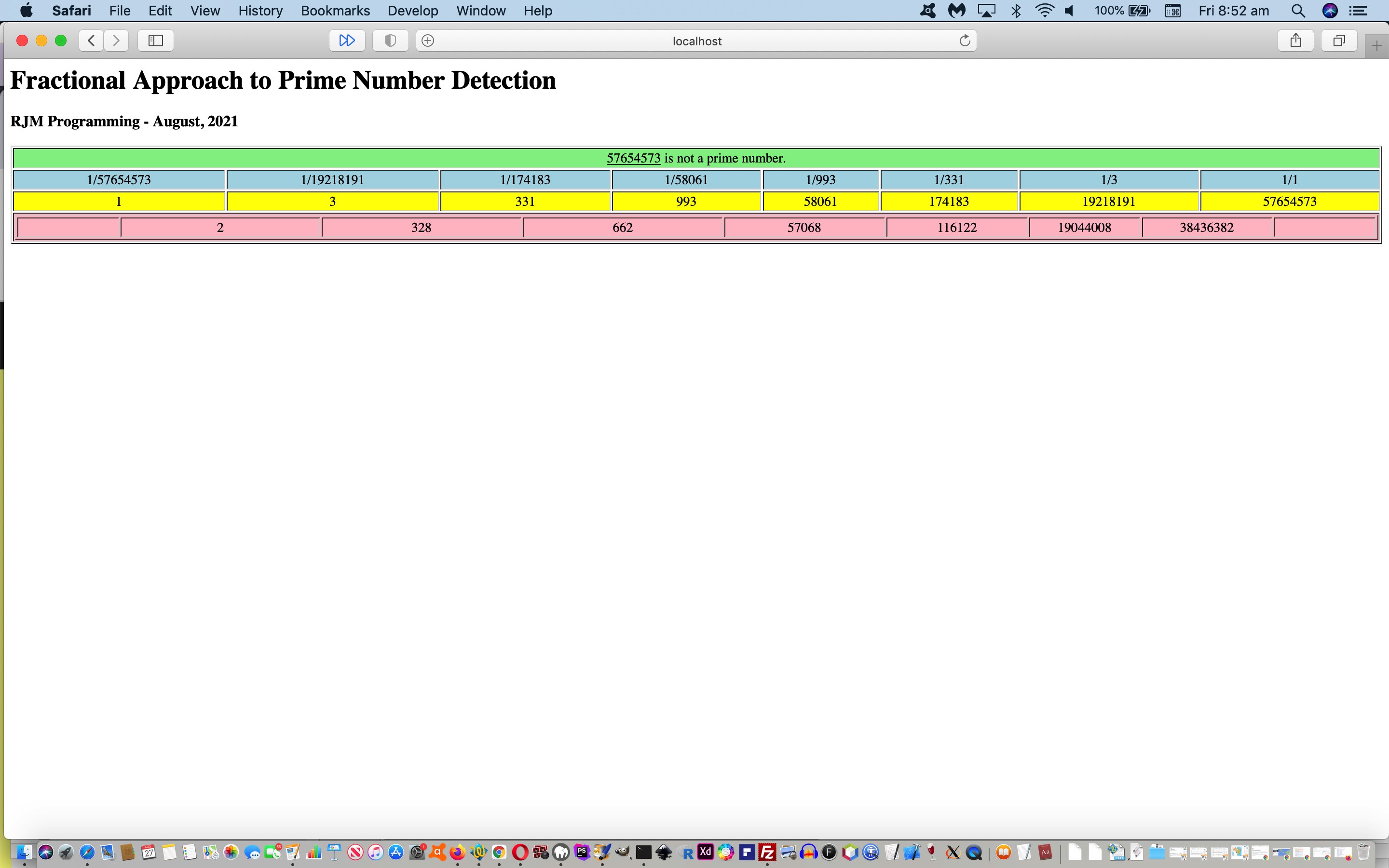
Onto the recent Prime Numbers Primer Tutorial we introduce some ideas regarding representing a fraction on a webpage, some a bit on the whimsical side, when it comes to matching emojis to ancient concepts, so that you can represent the fractional parts of our prime numbers web application in the following ways …
| Options | Display |
|---|---|
| supsub | sup numerator and sub denominator |
| boring | no sup nor sub nor i nor b |
| sup | sup numerator only |
| sub | sub denominator only |
| ib | italic numerator and bold denominator |
| bi | bold numerator and italic denominator |
| emoji | emoji |
| roman | roman numerals (thanks to https://stackoverflow.com/questions/9083037/convert-a-number-into-a-roman-numeral-in-javascript/9083076) |
| egyptian | egyptian (thanks to https://www.dummies.com/education/math/pre-algebra/10-alternative-numeral-and-number-systems/) |
| hexadecimal | hexadecimal (featuring the [number].toString(16) idea) |
We chose this tutorial and its associated web application to give an airing to some of those “little” (but often very useful) textual HTML elements …
- sup superscript
- sub subscript
- i italic
- b bold (or these days perhaps you should be moving to strong)
… the top two of which we think are very apt applied, optionally, but as the default arrangement, for the fractional values shown in the changed “proof of concept” fractional_prime.html live run link.
Previous relevant Prime Numbers Primer Tutorial is shown below.
We’ve been itching to do a “Prime Numbers Primer Tutorial” but haven’t found an interesting enough “in”. But I had occasion to want to count down an hour long period of time the other day, and wondered at the number patterns, or not, as the case may be that thinking about the positive integers involved, and whether they represent a prime number …
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.Prime Numbers Primer Tutorial
… or not. That whiled away that hour and made me think to involve fractions as well as these “prime number” considerations might make for a slightly interesting “take” on this “well worn” subject (or the uncharitable might say … “looking for patterns where there are none”). Our major Javascript function goes like …
function fcalc() {
var assessment=' is a prime number.';
var innards='', facline='<tr id=tr2></tr>', divline='<tr id=tr3></tr>', diffsline='<tr id=tr4><td colspan=' + divisors.length + '><table style="width:100%;text-align:center;" border=1><tr><td id=td0></td></TR></table></td></tr>';
var lastii=-1;
var huhti=1, rect=null, lastrect=null;
for (var ii=mynum; ii>=1; ii--) {
if (('' + eval(mynum / ii)).indexOf('.') == -1) {
divisors.push(ii);
if (eval('' + divisors.length) > 2) { assessment=' is not a prime number.'; }
facline=facline.replace('</tr>', '<td>1/' + ii + '</td></tr>');
divline=divline.replace('</tr>', '<td id=dt' + divisors.length + '>' + eval(mynum / ii) + '</td></tr>');
if (('' + lastii).indexOf('-') != -1) {
lastii=eval(mynum / ii);
} else {
diffs.push(eval(eval(mynum / ii) - lastii));
diffsline=diffsline.replace('</TR>', '<td id=td' + diffs.length + '>' + eval(eval(mynum / ii) - lastii) + '</td></TR>');
lastii=eval(mynum / ii);
}
}
}
innards+='<tr id=tr1><td colspan=' + divisors.length + '><a onclick=ask(); style="cursor:pointer;text-decoration:underline;">' + mynum + '</a><span id=shuh>' + assessment + '</span></td></tr>' + facline + divline + diffsline.replace(' colspan=0', ' colspan=' + divisors.length).replace('</TR>','<td id=xxx></td></tr>');
document.getElementById('mytable').innerHTML=innards;
while (document.getElementById('dt' + huhti)) {
rect=document.getElementById('dt' + huhti).getBoundingClientRect();
if (huhti == 1) {
document.getElementById('td0').style.width='' + eval(eval('' + rect.width) / 2) + 'px';
document.getElementById('xxx').style.width='' + eval(eval('' + rect.width) / 2) + 'px';
}
if (document.getElementById('dt' + eval(1 + huhti))) {
if (lastrect) {
//alert( eval(eval(eval('' + rect.x) - eval('' + lastrect.x)) / 2));
//document.getElementById('td' + huhti).style.left='' + eval(eval(eval('' + rect.left) - eval('' + lastrect.left)) / 2) + 'px';
document.getElementById('td' + huhti).style.width='' + lastrect.width + 'px';
} else {
document.getElementById('td' + huhti).style.width='' + rect.width + 'px';
}
}
lastrect=rect;
huhti++;
}
}
… for a “proof of concept” fractional_prime.html live run link for you to try, should you be curious.
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.