Is the Prime Numbers via Fractional Display web application of yesterday’s Prime Numbers Fractional Favicon Canvas Tutorial generic enough to consider giving it more scope for sharing and collaboration? We think so, and if you do too, you might want to see some Javascript code basis for the “midair feeling” Ajax/FormData methodology we adopt to make …
- email (via inline HTML) happen … and as an interactively created link for …
- SMS
… mode conduits of communication of this web application …
function emailit(nne) {
var smslist=[];
var tois='';
if (nne == null) { nne=''; }
if (nne.replace(',','@').replace(';','@').indexOf('@') != -1) {
document.getElementById('ito').value=nne;
var zhr = new XMLHttpRequest();
var zform=new FormData();
zform.append('inline', '');
while (nne.split(';')[0].split(',')[0].indexOf('@') == -1 && eval('' + nne.length) > 1) {
smslist.push(nne.split(';')[0].split(',')[0]);
nne=nne.replace(nne.split(';')[0].split(',')[0], '');
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
}
}
tois=nne.split(';')[0].split(',')[0].trim();
zform.append('to', nne.split(';')[0].split(',')[0]);
nne=nne.replace(nne.split(';')[0].split(',')[0], '');
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
}
while (nne.split(';')[0].split(',')[0].indexOf('@') == -1 && eval('' + nne.length) > 1) {
smslist.push(nne.split(';')[0].split(',')[0]);
nne=nne.replace(nne.split(';')[0].split(',')[0], '');
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
}
}
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
zform.append('cc', nne.split(';')[0].split(',')[0]);
nne=nne.replace(nne.split(';')[0].split(',')[0], '');
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
}
}
while (nne.split(';')[0].split(',')[0].indexOf('@') == -1 && eval('' + nne.length) > 1) {
smslist.push(nne.split(';')[0].split(',')[0]);
nne=nne.replace(nne.split(';')[0].split(',')[0], '');
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
}
}
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
zform.append('bcc', nne.split(';')[0].split(',')[0]);
nne=nne.replace(nne.split(';')[0].split(',')[0], '');
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
}
}
while (nne.split(';')[0].split(',')[0].indexOf('@') == -1 && eval('' + nne.length) > 1) {
smslist.push(nne.split(';')[0].split(',')[0]);
nne=nne.replace(nne.split(';')[0].split(',')[0], '');
if (eval('' + nne.length) > 1) {
nne=nne.substring(1);
}
}
zform.append('subj', 'Prime Numbers via Fractions');
//zform.append('body', '<html><head><style> #tr1 { background-color: lightgreen; } #tr2 { background-color: lightblue; } #tr3 { background-color: yellow; } #tr4 { background-color: pink; } td { height: 10%; } </style></head><body>' + document.body.innerHTML.replace(/NONE\;/g,'inline-block;').split('<iframe ')[0].replace(/\.\/fractional\_prime\.html/g, document.URL.split('?')[0].split('#')[0]) + '</body><html>');
zform.append('body', '<html><body>' + document.body.innerHTML.replace(/NONE\;/g,'inline-block;').split('<iframe ')[0].replace(/\.\/fractional\_prime\.html/g, document.URL.split('?')[0].split('#')[0]).replace('80vh;','40vh;').replace(' id="' + curmode + '"', ' id="' + curmode + '" selected') + '</body><html>');
if (tois != '') {
zhr.open('post', '//www.rjmprogramming.com.au/HTMLCSS/emailhtml.php', true);
zhr.send(zform);
}
if (eval('' + smslist.length) > 0) {
if (altc == '') {
altc=document.URL.split('#')[0].split('?')[0] + '?number=' + ('' + mynum).split('.')[0] + usuffix;
}
for (var ihj=0; ihj<eval('' + smslist.length); ihj++) {
//alert(smslist[ihj] + ' and altc=' + altc);
if (smslist[ihj].trim() != '') {
document.getElementById('asms').href='sms:' + ('' + smslist[ihj].trim()) + '&body=' + encodeURIComponent(altc);
if (document.getElementById('asms').title.indexOf('SMS ') == -1) {
document.getElementById('asms').title='SMS ' + ('' + smslist[ihj].trim());
} else {
document.getElementById('asms').title+=' and ' + ('' + smslist[ihj].trim());
}
document.getElementById('asms').click();
}
}
}
} else if (('' + nne.trim()) != '' && ('' + nne.trim()).replace(/0/g,'').replace(/1/g,'').replace(/2/g,'').replace(/3/g,'').replace(/4/g,'').replace(/5/g,'').replace(/6/g,'').replace(/7/g,'').replace(/8/g,'').replace(/9/g,'') == '') {
if (altc == '') {
altc=document.URL.split('#')[0].split('?')[0] + '?number=' + ('' + mynum).split('.')[0] + usuffix;
}
document.getElementById('asms').href='sms:' + ('' + nne.trim()) + '&body=' + encodeURIComponent(altc);
document.getElementById('asms').title='SMS ' + ('' + nne.trim());
document.getElementById('asms').click();
}
}
function aske() {
var nne=prompt('Please enter email address (comma separate an optional CC then BCC) and/or an SMS number?', '');
if (nne == null) { nne=''; }
emailit(nne);
}
The code above allows for a “mixed mode” of communication addresses if you want to send off an email and/or SMS … a feature we don’t remember coding for in the past, much.
A new emoji animated button flags this sharing functionality possibility for the changed “proof of concept” fractional_prime.html live run link.
Previous relevant Prime Numbers Fractional Favicon Canvas Tutorial is shown below.
Further to yesterday’s Prime Numbers Fractional Favicon Tutorial …
What’s the HTML5 canvas element got to do with web browser tab icon “favicon” graphic content?
Well, as per the excellent advice ideas on this webpage, thanks, we can use the canvas …
<canvas id="canvas" width=32 height=32 style="display:none;"></canvas>
… (static HTML, as above) element as a conduit to …
- [canvasContent].clearRect(0,0,32,32);
- [canvasContent].drawImage([imgObject],0,0,32,32); // via saved away data URI as per [canvas].toDataURL(“image/png”) … to a global internal Javascript array …
- enhance that content with some (canvas graphics, slightly everchanging) line work …
var datauris=[];
var img=null;
var canvas=null;
var context=null;
var ioffset=0, ifactor=1;
var rldone='';
function arsthen() {
var ij=0;
if (document.getElementById('myicon')) {
if (rldone != '') {
ij=eval(-1 + eval(-1 * eval('' + rldone.trim())));
}
if (eval('' + datauris.length) < 6) {
img = new Image();
img.onload = function() {
context.clearRect(0,0,32,32);
context.drawImage(img, 0, 0, 32, 32);
datauris.push(canvas.toDataURL('image/png'));
};
img.src='/favicon' + rldone.trim() + '.ico';
document.getElementById('myicon').href='/favicon' + rldone.trim() + '.ico';
} else {
if (1 == 1) {
img = new Image();
img.onload = function() {
context.clearRect(0,0,32,32);
context.drawImage(img, 0, 0, 32, 32);
var zz=0;
var tt=32;
zz=Math.abs(ioffset);
tt=eval(32 - Math.abs(ioffset));
if (ifactor == 1) {
ioffset++;
if (ioffset >= 14) {
ifactor=-1;
}
} else {
ioffset--;
if (ioffset <= 1) {
ifactor=1;
}
}
console.log('zz=' + zz + ' and tt=' + tt + ' and ioffset=' + ioffset);
// Thanks to https://www.geeksforgeeks.org/how-to-use-animation-on-favicon-image/
var linerGradient = context.createLinearGradient(zz, zz, tt, tt);
linerGradient.addColorStop(0, '#8be8a7');
linerGradient.addColorStop(1, '#297d4c');
context.strokeStyle = linerGradient;
context.lineWidth = 4;
context.beginPath();
context.moveTo(zz, zz);
context.lineTo(tt, zz);
context.moveTo(tt, zz);
context.lineTo(tt, tt);
context.moveTo(tt, tt);
context.lineTo(zz, tt);
context.moveTo(zz, tt);
context.lineTo(zz, zz);
context.stroke();
document.getElementById('myicon').href=canvas.toDataURL('image/png'); //datauris[ij];
};
img.src=datauris[ij];
} else {
document.getElementById('myicon').href=datauris[ij];
}
console.log('ij=' + ij + ' and datauris length is ' + datauris[ij].length);
}
if (rldone == '') {
rldone='-2';
} else if (rldone != rldone.trim()) {
rldone='' + eval(1 + eval('' + rldone.trim())) + ' ';
if (rldone == '-1 ') { rldone=''; }
} else {
rldone='' + eval(-1 + eval('' + rldone .trim()));
if (rldone == '-7') { rldone='-5 '; }
}
} else {
var fi=document.createElement('link');
fi.rel='icon';
fi.id='myicon';
if (rldone == '') {
if (datauris.length == 0) {
img = new Image();
img.onload = function() {
context.clearRect(0,0,32,32);
context.drawImage(img, 0, 0, 32, 32);
datauris.push(canvas.toDataURL('image/png'));
};
img.src='/favicon' + rldone.trim() + '.ico';
}
fi.href='/favicon' + rldone.trim() + '.ico';
rldone='-2';
} else {
if (eval('' + datauris.length) < 6) {
img = new Image();
img.onload = function() {
context.clearRect(0,0,32,32);
context.drawImage(img, 0, 0, 32, 32);
datauris.push(canvas.toDataURL('image/png'));
};
img.src='/favicon' + rldone .trim() + '.ico';
}
fi.href='/favicon' + rldone .trim() + '.ico';
rldone='' + eval(-1 + eval('' + rldone .trim()));
if (rldone == '-7') { rldone=''; }
}
document.head.appendChild(fi);
}
setTimeout(arsthen, 1000);
}
setTimeout(arsthen, 1000);
… while we are at it, reordering so that a white “favicon” no longer suddenly becomes an original “favicon” (a new paradigm part introduced, today, for the blog you are reading, also) - [link].href=[canvas].toDataURL(“image/png”);
Previous relevant Prime Numbers Fractional Favicon Tutorial is shown below.
So what’s the “favicon” in today’s blog posting title? If none the wiser, what about the (pretty much standalone Javascript) code below?
var rldone='';
function arsthen() {
if (document.getElementById('myicon')) {
document.getElementById('myicon').href='/favicon' + rldone + '.ico';
if (rldone == '') {
rldone='-2';
} else {
rldone='' + eval(-1 + eval('' + rldone));
if (rldone == '-7') { rldone=''; }
}
} else {
var fi=document.createElement('link');
fi.rel='icon';
fi.id='myicon';
if (rldone == '') {
fi.href='/favicon' + rldone + '.ico';
rldone='-2';
} else {
fi.href='/favicon' + rldone + '.ico';
rldone='' + eval(-1 + eval('' + rldone));
if (rldone == '-7') { rldone=''; }
}
document.head.appendChild(fi);
}
setTimeout(arsthen, 1000);
}
setTimeout(arsthen, 1000);
If you’ve guessed “is it something to do with that little icon to the left of the web browser tabs?” you’d be rightcorrect. In fact, we’re trying to apply some rudimentary animation to it today …
- not by involving any animated GIF files (though that may work) … but … and this is not the only way … and this does not work everywhere, but …
- use Javascript DOM to periodically change the graphic content of our changed “proof of concept” fractional_prime.html live run link on top of yesterday’s Variety of Prime Numbers Fractional Forms Tutorial‘s progress
In fact, it’s a bit obscure, perhaps, but we image edited …
| Started with favicon.ico … | … then created favicon-2.ico … | … then created favicon-3.ico … | … then created favicon-4.ico … | … then created favicon-5.ico … | … then created favicon-6.ico … |
|---|---|---|---|---|---|
… not with the Inkscape (vector) image editor we created favicon.ico with, but, good ol’ Gimp, because all the “then created” bits just involved “whiting” some non-white pixels from a previous incarnation via Gimp …
- zoom in a lot …
- set foreground and background colours to white …
- set the “Bucket Fill Tool” … then …
- click on the next non-white area of image to whiten via a “Bucket Fill Tool” click (causing contiguous pixels of that same non-white colour to become white)
- File -> Export As -> Icon Details … 4pp, 1-bit aplha, 16-slot pallette … to that new name of image file (as mentioned above)
… as you can see a bit of with today’s animated GIF presentation tutorial picture.
We also applied that Javascript DOM way of doing this to the blog you are reading, and RJM Programming’s Landing Page (and friends).
Previous relevant Variety of Prime Numbers Fractional Forms Tutorial is shown below.
Previous work of Prime Numbers Fractional Forms Tutorial and preceeding dealt with …
- your garden variety prime number … but then we read this Various Types of Numbers which set us straight at categorizing also …
- even numbers (only 2 out of all the even positive counting numbers, is a prime number) … but
evenoddly … - odd numbers … and back to prime number interest …
- composite numbers (ie. not a prime number) …
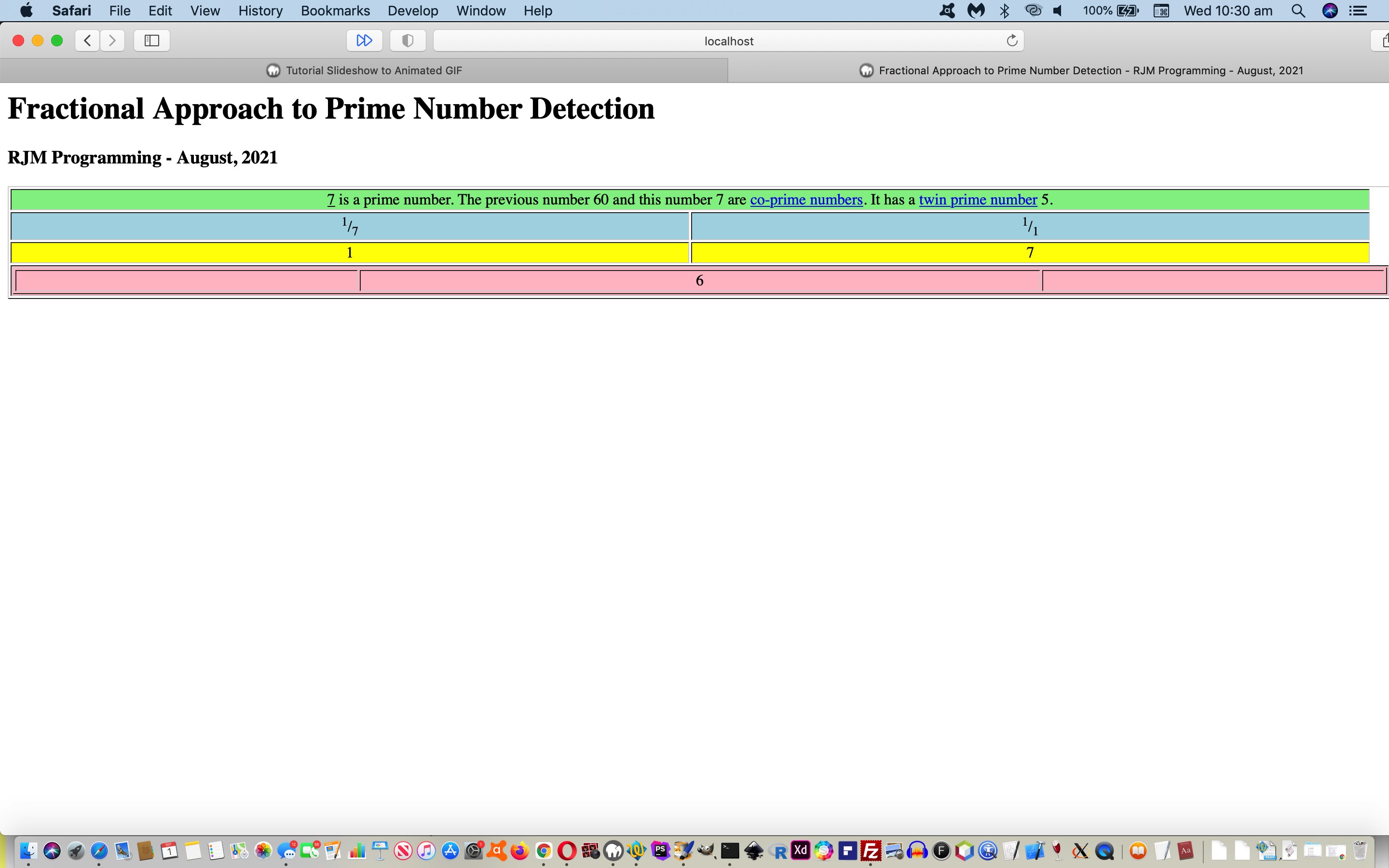
- co-prime numbers …
Co-prime Numbers
Two numbers are said to be co-prime if they do not have a common factor other than 1 or two numbers whose HCF is 1 called co-prime numbers.… which by that definition do not necessarily have to be prime numbers themselves,
eventualoddly - twin prime numbers …
Twin Prime Numbers
Twin prime numbers are the two prime numbers whose difference is 2.… the (coding) solution for which centres around the use of HTML iframe elements …
<iframe id=iupper style='display:none;' onload='fupper(this);' src='./fractional_prime.html'></iframe>
<iframe id=ilower style='display:none;' onload='flower(this);' src='./fractional_prime.html'></iframe>
… and their onload event Javascript logics …
var first=0, acontou=null, acontoi=null;
function fupper(iois) {
if (first >= 2) {
acontou = (iois.contentWindow || iois.contentDocument);
if (acontou != null) {
if (acontou.document) { acontou = acontou.document; }
if (acontou.body != null) {
if (acontou.body.innerHTML.indexOf(' is a ' + 'prim' + 'e ') != -1) {
document.getElementById('shuh').innerHTML+=' It has a <a target=_blank href=https://www.math-only-math.com/various-types-of-numbers.html>twin prime number</a> ' + decodeURIComponent(iois.src.split('number=')[1].split('&')[0].split('#')[0]).split('.')[0] + '. ';
}
}
}
}
first++;
}
function flower(iois) {
if (first >= 2) {
acontoi = (iois.contentWindow || iois.contentDocument);
if (acontoi != null) {
if (acontoi.document) { acontoi = acontoi.document; }
if (acontoi.body != null) {
if (acontoi.body.innerHTML.indexOf(' is a ' + 'prim' + 'e ') != -1) {
document.getElementById('shuh').innerHTML+=' It has a <a target=_blank href=https://www.math-only-math.com/various-types-of-numbers.html>twin prime number</a> ' + decodeURIComponent(iois.src.split('number=')[1].split('&')[0].split('#')[0]).split('.')[0] + '. ';
}
}
}
}
first++;
}
If you are curious here, try out our changed “proof of concept” fractional_prime.html live run link.
Previous relevant Prime Numbers Fractional Forms Tutorial is shown below.
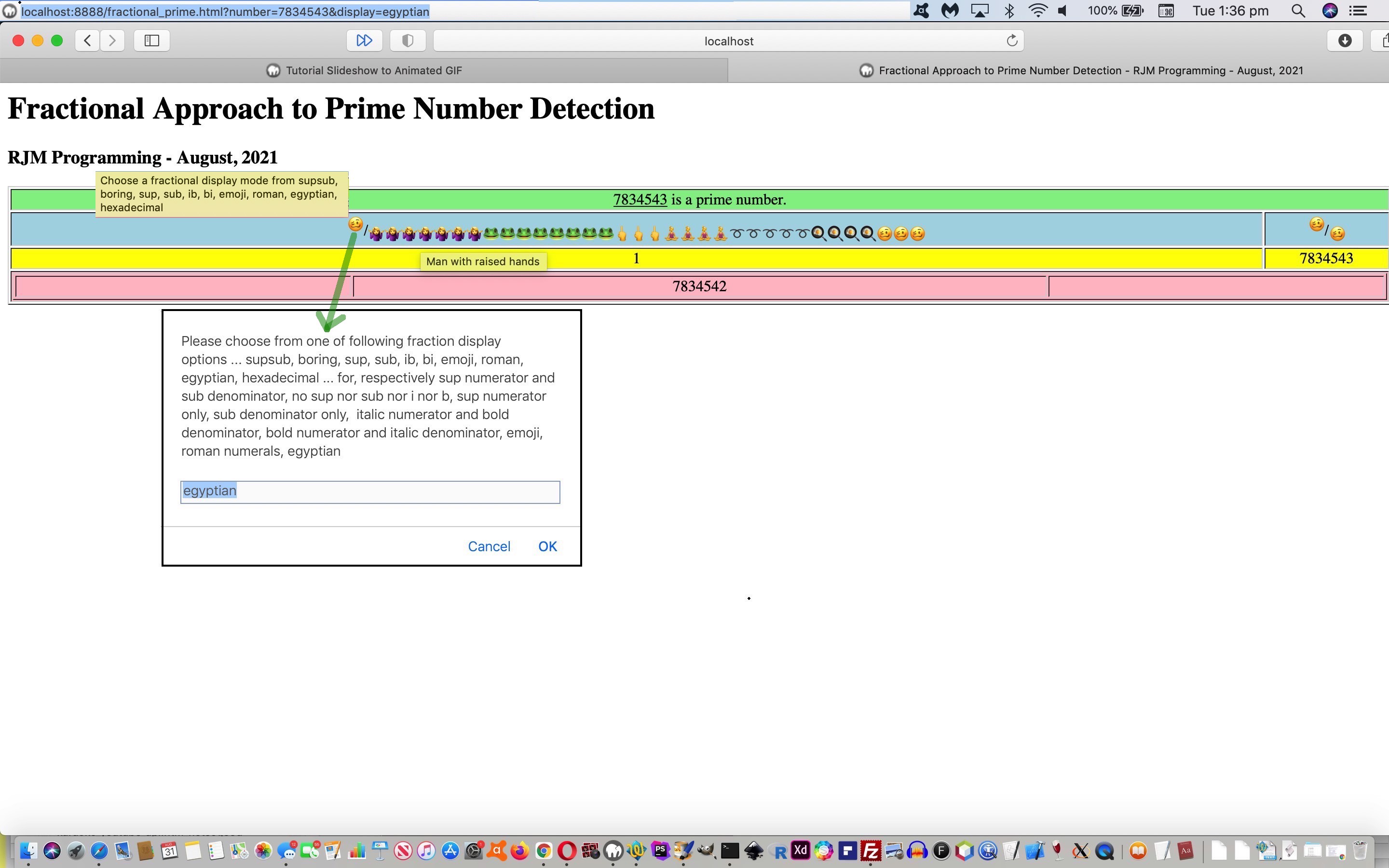
Onto the recent Prime Numbers Primer Tutorial we introduce some ideas regarding representing a fraction on a webpage, some a bit on the whimsical side, when it comes to matching emojis to ancient concepts, so that you can represent the fractional parts of our prime numbers web application in the following ways …
| Options | Display |
|---|---|
| supsub | sup numerator and sub denominator |
| boring | no sup nor sub nor i nor b |
| sup | sup numerator only |
| sub | sub denominator only |
| ib | italic numerator and bold denominator |
| bi | bold numerator and italic denominator |
| emoji | emoji |
| roman | roman numerals (thanks to https://stackoverflow.com/questions/9083037/convert-a-number-into-a-roman-numeral-in-javascript/9083076) |
| egyptian | egyptian (thanks to https://www.dummies.com/education/math/pre-algebra/10-alternative-numeral-and-number-systems/) |
| hexadecimal | hexadecimal (featuring the [number].toString(16) idea) |
We chose this tutorial and its associated web application to give an airing to some of those “little” (but often very useful) textual HTML elements …
- sup superscript
- sub subscript
- i italic
- b bold (or these days perhaps you should be moving to strong)
… the top two of which we think are very apt applied, optionally, but as the default arrangement, for the fractional values shown in the changed “proof of concept” fractional_prime.html live run link.
Previous relevant Prime Numbers Primer Tutorial is shown below.
We’ve been itching to do a “Prime Numbers Primer Tutorial” but haven’t found an interesting enough “in”. But I had occasion to want to count down an hour long period of time the other day, and wondered at the number patterns, or not, as the case may be that thinking about the positive integers involved, and whether they represent a prime number …
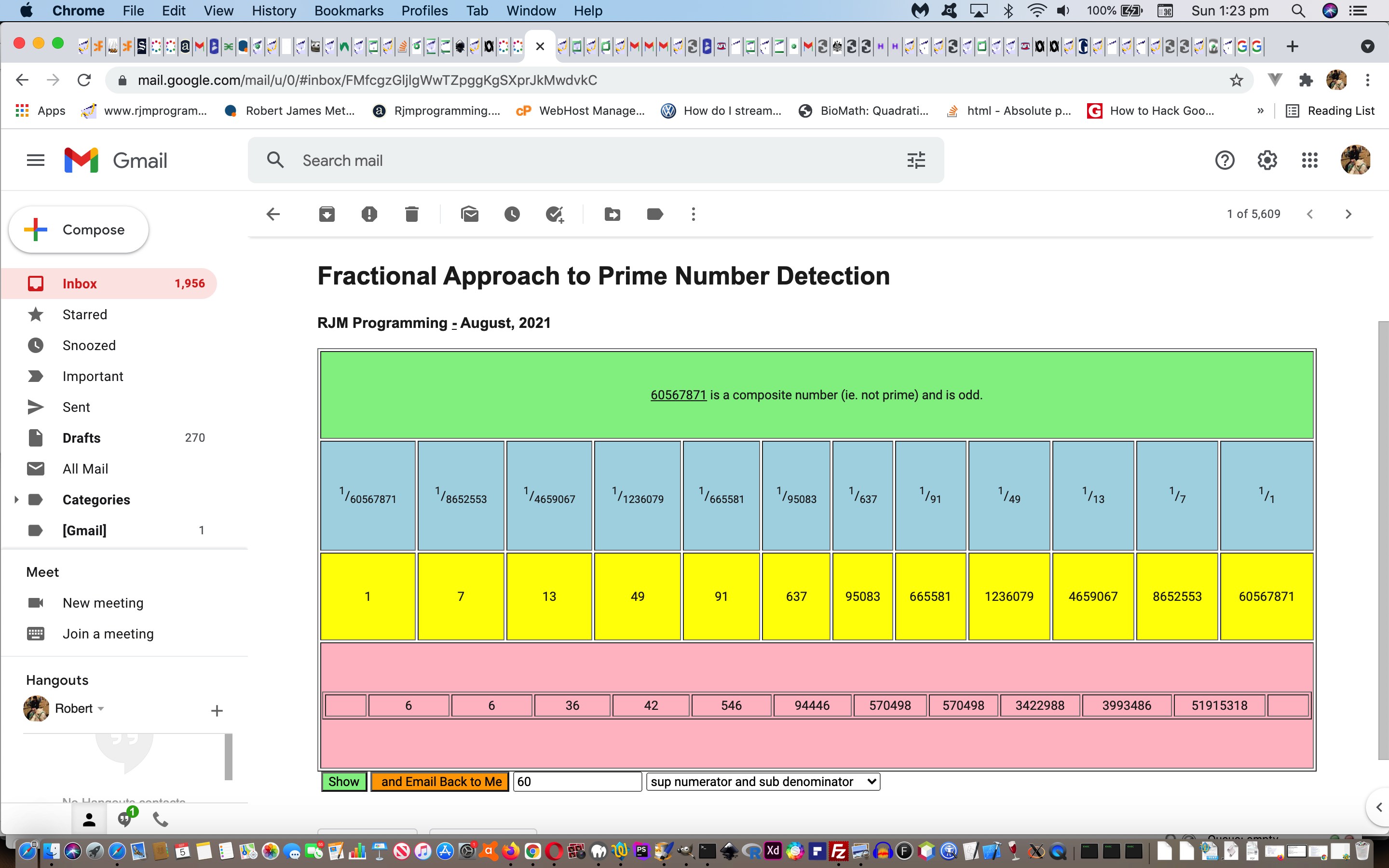
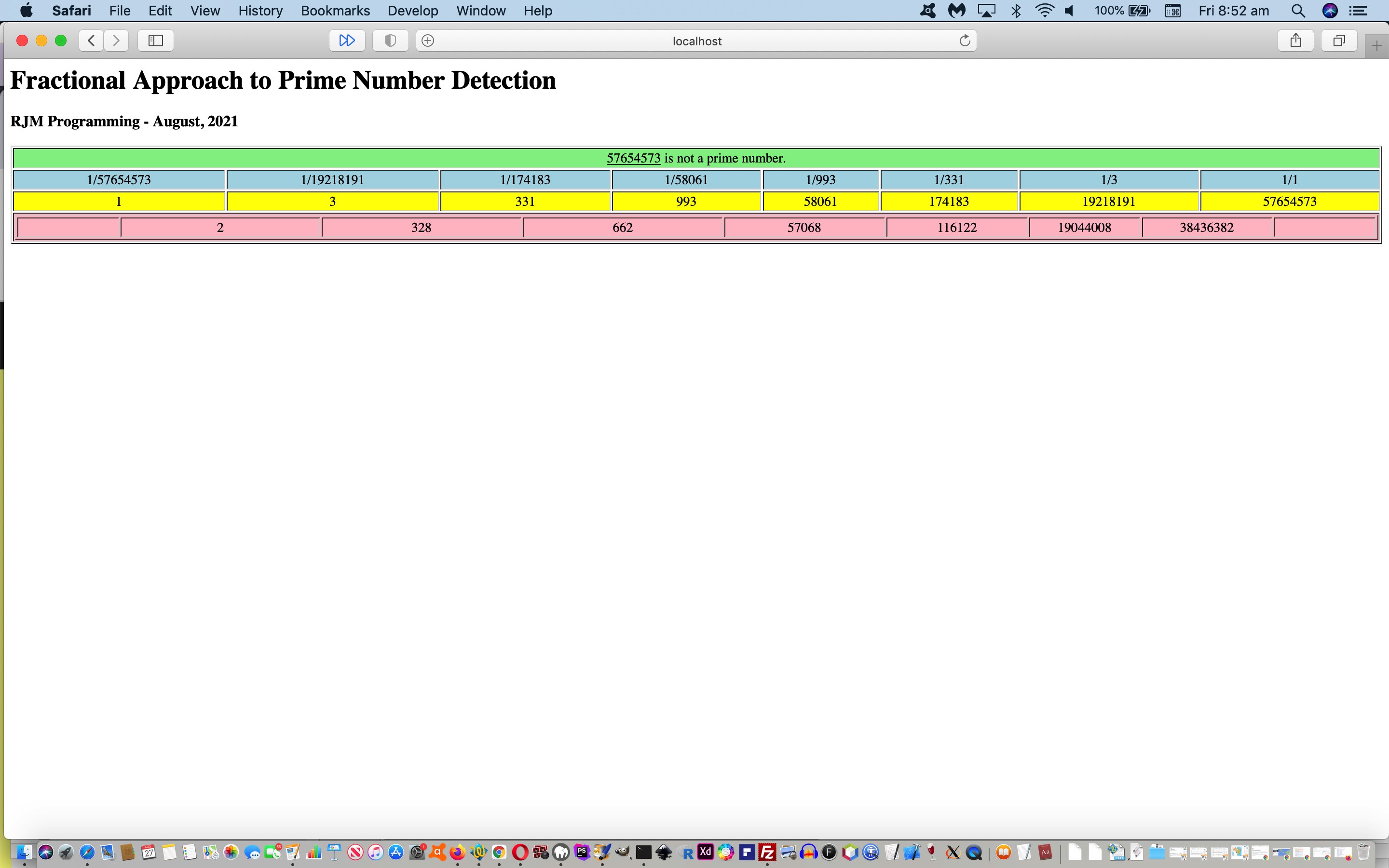
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.Prime Numbers Primer Tutorial
… or not. That whiled away that hour and made me think to involve fractions as well as these “prime number” considerations might make for a slightly interesting “take” on this “well worn” subject (or the uncharitable might say … “looking for patterns where there are none”). Our major Javascript function goes like …
function fcalc() {
var assessment=' is a prime number.';
var innards='', facline='<tr id=tr2></tr>', divline='<tr id=tr3></tr>', diffsline='<tr id=tr4><td colspan=' + divisors.length + '><table style="width:100%;text-align:center;" border=1><tr><td id=td0></td></TR></table></td></tr>';
var lastii=-1;
var huhti=1, rect=null, lastrect=null;
for (var ii=mynum; ii>=1; ii--) {
if (('' + eval(mynum / ii)).indexOf('.') == -1) {
divisors.push(ii);
if (eval('' + divisors.length) > 2) { assessment=' is not a prime number.'; }
facline=facline.replace('</tr>', '<td>1/' + ii + '</td></tr>');
divline=divline.replace('</tr>', '<td id=dt' + divisors.length + '>' + eval(mynum / ii) + '</td></tr>');
if (('' + lastii).indexOf('-') != -1) {
lastii=eval(mynum / ii);
} else {
diffs.push(eval(eval(mynum / ii) - lastii));
diffsline=diffsline.replace('</TR>', '<td id=td' + diffs.length + '>' + eval(eval(mynum / ii) - lastii) + '</td></TR>');
lastii=eval(mynum / ii);
}
}
}
innards+='<tr id=tr1><td colspan=' + divisors.length + '><a onclick=ask(); style="cursor:pointer;text-decoration:underline;">' + mynum + '</a><span id=shuh>' + assessment + '</span></td></tr>' + facline + divline + diffsline.replace(' colspan=0', ' colspan=' + divisors.length).replace('</TR>','<td id=xxx></td></tr>');
document.getElementById('mytable').innerHTML=innards;
while (document.getElementById('dt' + huhti)) {
rect=document.getElementById('dt' + huhti).getBoundingClientRect();
if (huhti == 1) {
document.getElementById('td0').style.width='' + eval(eval('' + rect.width) / 2) + 'px';
document.getElementById('xxx').style.width='' + eval(eval('' + rect.width) / 2) + 'px';
}
if (document.getElementById('dt' + eval(1 + huhti))) {
if (lastrect) {
//alert( eval(eval(eval('' + rect.x) - eval('' + lastrect.x)) / 2));
//document.getElementById('td' + huhti).style.left='' + eval(eval(eval('' + rect.left) - eval('' + lastrect.left)) / 2) + 'px';
document.getElementById('td' + huhti).style.width='' + lastrect.width + 'px';
} else {
document.getElementById('td' + huhti).style.width='' + rect.width + 'px';
}
}
lastrect=rect;
huhti++;
}
}
… for a “proof of concept” fractional_prime.html live run link for you to try, should you be curious.
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.
If this was interesting you may be interested in this too.